Brain scores don't mean what we think they mean (maybe)

ANNs 🤝 BNNs

Artificial neural networks trained to perform the same tasks as humans–image classification, self-motion prediction, building a cognitive map of the environment–tend to converge to representations that are similar to the brain. This is a central finding of the field of task-driven neural networks, also called neuroconnectionism.

Representations in ANNs can be related to representations in BNNs through the methods of task-driven neural networks

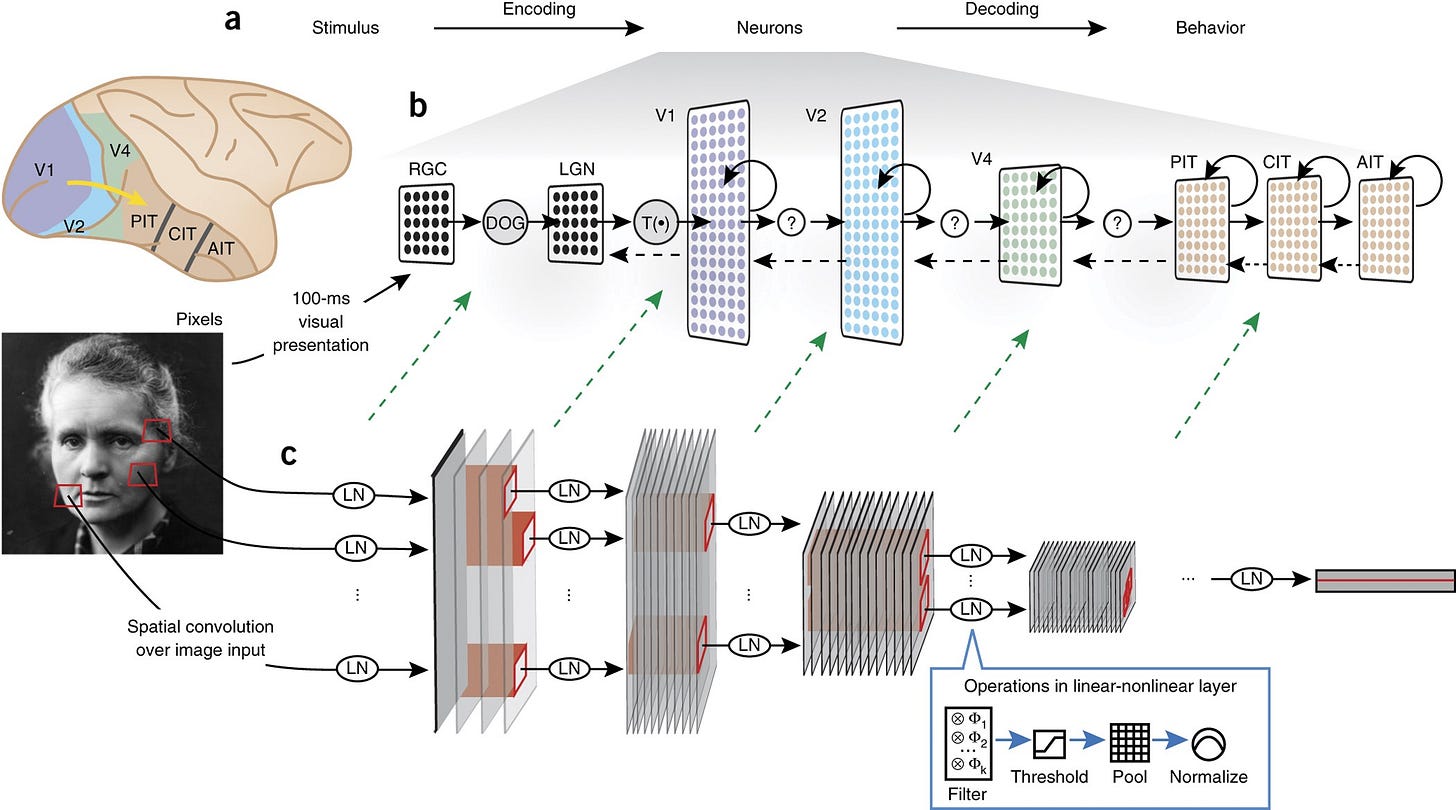
Linear regression is a well-accepted way of comparing artificial neural networks and brain activity (I wrote a tutorial-like intro here). Here’s how that usually goes:

• You collect lots of responses from the brain in response to stimuli (images, sounds, etc.)

• You do the same for an ANN

• You regress the ANN onto the brain, keeping the weights of the ANN fixed

• How well that regression works in predicting data in a validation fold tells you something how good a model of the brain is that ANN

Or does it? The position paper Maximizing Neural Regression Scores May Not Identify Good Models of the Brain argues that, well, it’s not that simple. There was a slew of activity on X¹ about the paper: some supportive, some negative, some sympathetic but saying that the paper went too far in the skeptical direction and overstated their argument. I will try to synthesize the discussion here and give some context so you can navigate this field.

My TL;DR: Neural scores don’t always mean what we think they mean. When neural scores are calculated between brains and the highly overparametrized representations of neural networks for a small number of stimuli, we have to carefully interpret the scores.

Breaking down the argument in Schaeffer et al. (2024)

Schaeffer and co. build an argument that neural regression score maximization doesn’t tell you which model is more like the brain. The argument goes like this:

1. Dimensionality is highly predictive of neural scores. Big networks with many features that cover a lot of ground generally match the brain better than small networks with low dimensionality. This conjecture was first made a few years ago to explain some puzzling results in entorhinal cortex and hippocampus (Schaeffer et al. 2022; although see Aran Nayebi’s rejoinder on X), and others found congruent results (e.g. Elmoznino and Bonner, 2022).

2. Neural scores are a reflection of the inductive biases of linear regression.

The effective dimensionality argument (1)–bigger is better–is intuitively attractive, but it’s wrong. While there’s some correlation between dimensionality and neural scores, the exact relationship is explained by the more subtle spectral theory of regression by Canatar et al. (2023), an excellent paper. It’s not just effective dimensionality (=big network good) that matters; it’s also the projections of the eigenvectors of the design matrix on the observations (=bigger not always better). To put it in the words of Mick Bonner: “High effective dimensionality alone is not sufficient to yield strong performance”.

Neural scores in the interpolation regime

What about the second point on the inductive biases of regression? I wish the authors had focused more on this, because it is an important and subtle point. When you really, deeply think about it, it is strange that we:

1. probe brains and models with hundreds of stimuli

2. map models to brains using linear regressions with thousands, sometimes millions of parameters

3. use those to differentiate between different models

The classic statistical viewpoint says that in this overparametrized regime, there is no unique solution to the linear regression. Equivalently, an infinite number of regressions could fit the data equally well, and you need assumptions to solve this degeneracy. The assumptions must be matched to the problem at hand and they influence the outcome of statistical comparisons.

From Canatar et al. M can be much, much larger than P.

Now, Schaeffer et al. don’t spell out why the inductive biases of linear regression might be problematic. It’s worth going back to spectral theory to understand why. Canatar et al. study the highly overparametrized regime (P stimuli << M units), where there are far more units (i.e. neurons, design matrix columns) than there are stimuli (i.e. observations, rows of the design matrix). Their theory is valid when there is no observation noise and the mapping between stimuli and neurons is static. They define the generalization error by chopping up the full design matrix into train and test. The generalization error is the result of testing on the test set with the linear regression weights inferred on the train set. With their definition, the generalization error must go be exactly zero as the proportion of training examples tends to 100% (remember, no noise!). You can see this, for example, in their figure SI.4.1.

From Canatar et al. (2023). Under their training scenario, the error goes to 0 when the proportion of the traing

In this setup, all models eventually get to 0 error. The path that models take to that zero error is a bit unintuitive, and it doesn’t map neatly into the usual schema of low error = good model that aligns well to the brain, high error = bad model that is unlike the brain. It depends on the details of the spectrum of the model activations matrix. For example, in the plot above the right, layer 3 and layer 4 swap places depending on the proportion of the data in the train and test set. That nonmonoticity is the product of the inductive biases of linear regression, not so much whether a model is brain-like or not.

TL;DR: take your scores with a grain of salt and use multiple lines of evidence to show that an ANN is like the brain. In the highly overparametrized regime, neural scores can have an unintuitive and complex relationship to the thing we ultimately care about: how well-matched an ANN is to the brain.

Contra Goodhart’s law

What happens when we overinterpret and hyperfocus on a single fixed metric? One take on X is that “as the field optimizes against a fixed proxy metric [which doesn’t fully capture brain similarity], the field begins Goodharting”. Goodhart’s law states that a metric that becomes an objective ceases to be a good metric.

So, are we hacking our metrics? I don’t think so. One pattern that’s associated with Goodhart’s law is that benchmarks get quickly saturated as people teach to the test, as is the case with LLMs. If we were Goodharting, the metrics would go only one way: up. But if you look at the history of vision BrainScore in particular, the metrics have stayed relatively stable over the years, perhaps even decreasing.

To be clear, this is not a good thing either! We want our theories to rise in accuracy over time so that we get ever closer to the truth! This is a point that I investigate in detail in the roadmap on neuroscience for AI safety that we recently published. Ideally, we’d be able to measure a low-noise gradient in model space to uncover more brain-like models over time. So far, we haven’t found great ways of doing that, which is a core problem for the field. We propose a few different lines of research that could help leapfrog this problem. In any case, I don’t think that it’s true that we are falling pray to Goodhart’s law.

Maybe many metrics aren’t good either

The singular focus on the flaws of one particular metric, in one regime, can make us forget about how neural scores are often used in practice. Neural regression scores are often tested out-of-distribution, which the in-distribution setup of Canatar et al. doesn’t cover. And we often use more metrics than just linear regression. Using more metrics–RSA, DSA, CKA, looking at tuning curves, one-to-one-mappings–is a commonly suggested way of avoiding becoming overly reliant on a single top-line metric. This has now become a best practice in the field: many models, many datasets, and ideally many metrics, each testing the model along different axes of variance. Although many papers still focus on one model and metric to their detriment, there are plenty of examples of papers that build a more compelling story around comprehensive testing, including Zhuang et al. (2021), Mineault et al. (2021), and Conwell et al. (2023).

Except… sometimes the metrics don’t agree and the conclusions are quite sensitive to the choice of metric. This was the conclusion in Soni et al. (2024) and Klabunde et al. (2024). That’s worrisome.

Metrics can vary a lot in how they rank different models. No metric does universally better than any other

My best guess for why this is boils down to two things:

1. Bad metrics: Some of the metrics are genuinely not good, or not used in practice, which adds noise to the rankings and inflates the extent of the problem.

2. P << M: there are many fewer stimuli than the dimensionality of the activations. That means the comparisons rely on inductive biases which are introduced in subtle and unintuitive ways. With a small number of stimuli, you don’t get good coverage of the distribution of inputs either.

The first point is solvable; Alex Williams and his group, among others, have been very active in finding axiomatically good metrics (e.g. this work on shape metrics). But the P << M problem remains.

What else can we do?

If the true underlying problem is overparametrization and the subtle inductive biases that are introduced to avoid the issues that come with overparametrization, maybe we ought to do things differently. What are some potential solutions?

1. Increase P. We should measure the responses to more and higher entropy stimuli.

2. Target stimuli better. Instead of wasting a big chunk of the P on constraining dimensions of the models we don’t care about, use targeted stimuli designed to maximally differentiate models. This is the solution proposed by Golan et al. (2020).

3. Decrease M. Use more constrained functions to map from ANN to brains.

Many people have argued for 1 and 2, and they’re pretty uncontroversial. Here I’ll try to make an argument in favor of 3, which I haven’t seen before. With 3–using a highly constrained set of weights–we’re also introducing an inductive bias, but we’re making it explicit. Even in this day and age of large-scale models with millions of parameters, P >> M is a viable regime. For example, the models explored by Lurz et al. (2021) have M < 100, but P up to 16,000. All it takes is a highly contained receptive field model to get into the classic regime.

It might seem like we’re skipping over the beautiful theory of double descent, but in fact the overparametrized regime (the double descent regime) doesn’t always lead to better solutions when there’s noise in the observations (see this tutorial for example). While the theory of Canatar et al. (2023) has a large surface, it assumes no noise in the measured responses. We have a theory of scaling laws for linear regression in the underparametrized, noisy setting in the NeuroAI safety roadmap. I’d love to see an extension that fuses the theory of Canatar and ours.

Parting words

All else being equal, line goes up=good

A model that explains more of the variance is better than a model that explains less of the variance, all else being equal. Maximizing explained variance is the way to go if we want to learn digital twins of the sensory cortex and control population activity. But a model that accounts for more variance in the brain is not necessarily a better model of the brain. And it’s easy to read more into a single score than what is warranted.

Antonello and Huth (2024) report that a next-token prediction objective and a German-to-English translation objective lead to representations that are equally good at predicting brain responses to podcasts in unilingual English speakers; the authors argue that “the high performance of these [next token prediction] models should not be construed as positive evidence in support of a theory of predictive coding [...] the prediction task which these [models] attempt to solve is simply one way out of many to discover useful linguistic features”.

Structurally, I think that what we want is for our scores to point us the way: to tell us where to look for more brain-like models on the mountain which is model space. But the scores are noisy and our hill-climbing is treacherous. Until we can get to p → ♾️, we will have to carefully consider the value of our models and scores.

Acknowledgements: Thanks to Shahab Bakhtiari, Aran Nayebi and Tim Kietzmann for reviewing this piece. Aran has an insightful comment on openreview breaking down the paper’s claims in detail.

1. This article has been sitting in my drafts for a couple of months, before the exodus to bsky. Apologies for the tardiness.