Gflownets: sampling on sets & graphs
A new family of sampling methods for complex structures that's 50% MCMC and 50% RL
NeuroAI scientists have to keep up with two literatures: neuro and ML. With ML in particular, with its culture of short conference papers, you have to contend with a torrent of breakthroughs and instantly obsolete results. How do you separate the wheat from the chaff?
Workshops! ML doesn’t do reviews, but it does have a culture of running thematically-themed workshops. A neuroscientist with some ML exposure can go to one of these and get the gist, which is not always the case for the talk tracks at most ML conferences.
I went to the gflownet workshop at Mila last week and returned delighted. Gflownets are something of a Mila specialty, having been introduced in a paper led by Emmanuel Bengio–Yoshua Bengio’s son–in 2021. Powerful but pretty obscure outside of Mila, gflownets have a ton of potential as samplers in otherwise intractable problems. They’ve proved quite powerful in other domains like drug discovery and materials science, and I hope someday soon in neuroscience. Here is my quick intro to these models to get you up to speed.
What’s a gflownet anyway?
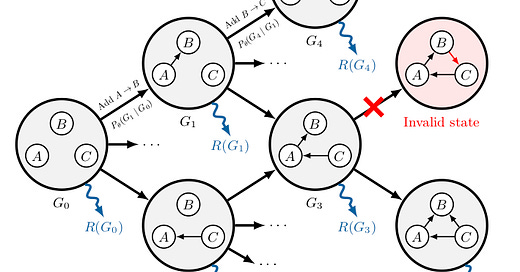
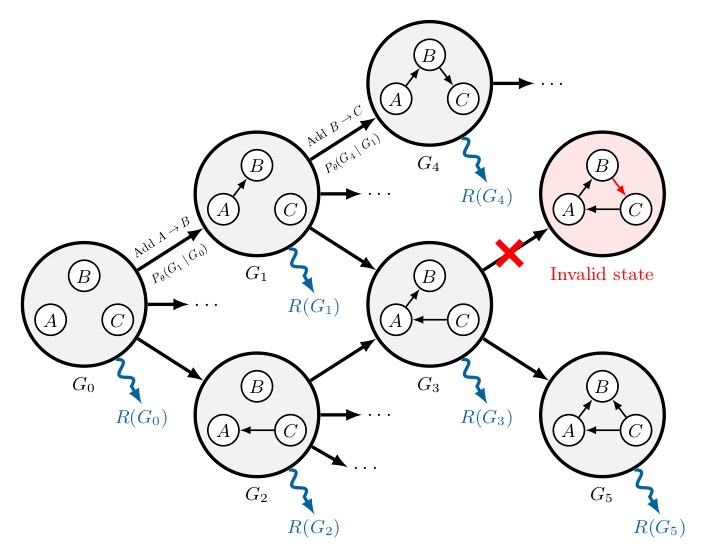
Gflownets, short for generative flow network, are a class of algorithms for sampling from a probability distribution. Like rejection sampling, slice sampling, or MCMC, gflownets sample from arbitrary (unnormalized) distributions. They’re particularly well-suited for sampling from objects with compositional structure, like sets, trees, and graphs.
Gflownets differ from classic sampling algorithms in that they’re trained using a supervised loss. Training a gflownet proceeds in the style of online reinforcement learning: you use a variant of an amortized inference network F to generate a sample with the current (bad) policy, evaluate the reward (i.e. the unnormalized likelihood of the sample), and adjust the weights of that network F to get better samples eventually. At convergence, the gflownet can be used to sample very cheaply from the target distribution–amortized inference.
Sampling in a gflownet looks a lot like traversing the state/action space as a reinforcement learning agent. Let’s say you want to sample from a gflownet trained to generate sets of characters of the Latin alphabet. You might start with the empty set ∅. A neural network with a softmax output F(·, ∅) would be used to decide whether to add one of the 26 characters or the stop character □, i.e. using a multinomial sample. Let’s say you sample the letter M. Then you would evaluate the network again, this time on F(·, {M}); and so on until you get a set of letters from 0 to 26 characters long.
Let’s talk about the name: generative flow networks. One key property of the sampler, once trained, is that the amount of probability flowing through one of the intermediate states of the sampler is the same as the outgoing probability. This is like (physical flow) in a river network: water in, water out. Thus, flow. The net in gflownets does not refer to a neural net. It refers instead to the Markov decision process (MDP) which leads to a sample, itself a network. Calling them gMDPs or just generative flows would be a little less confusing IMO. Naming is hard.
Grokking gflownets
As you can see, gflownets mix concepts from two different fields: sampling and reinforcement learning. It’s not that the concepts are really hard to grasp in and of themselves, it’s that gflownets arrange them in unusual ways which can make them hard to grok. You need to sit down with these ideas and let them simmer for a little bit to put them all together. The workshop did a really good job of presenting the background from the two fields to help bridge the gap.
Another barrier to gflownet adoption is that it can be hard to know all the tricks people use to make them work in practice. There’s a well of esoteric knowledge, and it hasn’t yet been translated into an easy-to-digest form (i.e. software that works out of the box). This will happen in due time.
I don’t recommend getting started with gflownets by reading the original paper, or the follow-up gflownet foundations paper; they’re hard to understand and are partly obsolete. Instead, I recommend streaming Day 2 of the workshop for a nice, self-contained intro to the field. There are two accompanying coding tutorials, one for discrete modelling and the other for continuous modelling. The gflownet website contains many other great resources. Once you’ve gone through those, would highly recommend this awesome list.
Losses
One prime example of a footgun in gflownets is choosing the right loss. The loss that is optimized during training is a consistency loss that says that inflows to a node in the decision network are similar to the outflows. This is basically a credit assignment problem: at the end of the process of sampling, you get a sample of a certain probability, and you’re trying to nudge the network such that you would have taken the right branches in the decision tree to get samples which match the probability distribution. Similar to the Bellman equation in reinforcement learning, there are many ways of writing down consistency losses.
You’re going to be tempted to read the first gflownet paper–or maybe the second!–and implement that, and that’s a bad idea. The three most frequently discussed losses are:
Flow loss. This is a (log) version of the temporal difference (TD) algorithm. It was originally introduced in the first gflownet paper (Bengio et al 2021a), but it doesn’t converge very well in practice, so it’s not really used anymore.
Detailed balance loss. Some of you familiar with MCMC will recognize this term. In this case, we parametrize both a forward function F_F and its converse backward function F_B such that probabilities match when traversing the tree forward and backward. It was introduced in the gflownet Foundations paper (Bengio et al. 2021b).
Trajectory balance. This algorithm, introduced in Malkin et al. (2022), does credit assignment on an entire trajectory. That’s the one that is currently recommended as a starting point.
This is the trajectory loss as defined in Malkin et al. (2022):
Here, P_F and P_B are forward and backward flow functions, and Z is the partition function, which is a trainable parameter. With that in hand, training a gflownet is pretty straightforward:
Extensions
You can condition your gflownets, similar to how you would condition a diffusion model
You can train a gflownet with observed samples rather than through an environment. This is called MLE-GFN.
Gflownets work naturally with discrete objects (sets, graphs, trees, etc), but you can extend them to continuous objects. This is important in practice, because many real problems need both discrete and continuous parameters. The math and the implementation difficulties really ramp up in continuous space. This is still a very active area of research.
Software
There are ~3 implementations of gflownet out there, all of which originated around Mila. None of these has yet reached escape velocity but together they should cover a range of use cases.
torchgfn. Salem Lahlou, et al. This is a low-level library with all the primitives necessary to implement discrete and continuous environments, as well as flow balance, detailed balance, trajectory balance and subtrajectory balance. It contains clean, reference implementations.
alexhernandezgarcia/gflownet. Alex Hernandez-Garcia. This one is aimed at a higher level of abstraction with more complex environments, so a good place to start for an applied scientist. It has some nice facilities for logging (hydra, wandb). Probably the most active repo in terms of commits, and used internally for several papers.
recursionpharma/gflownet. Emmanuel Bengio. This one is specialized for pharma and drug discovery applications.
Potential applications in neuroscience
Gflownets allow you to do something important and in general intractably difficult: sampling from funky distributions. You need sampling when uncertainty is an object of interest. Lots of problems can be solved by a good sampler: generating samples, estimating the parameters of a model, estimating the evidence for Bayesian model comparison, and estimating the uncertainty of a learned structure. To be clear, I haven’t seen gflownets applied in neuroscience yet, but it’s something that people are highly interested in.
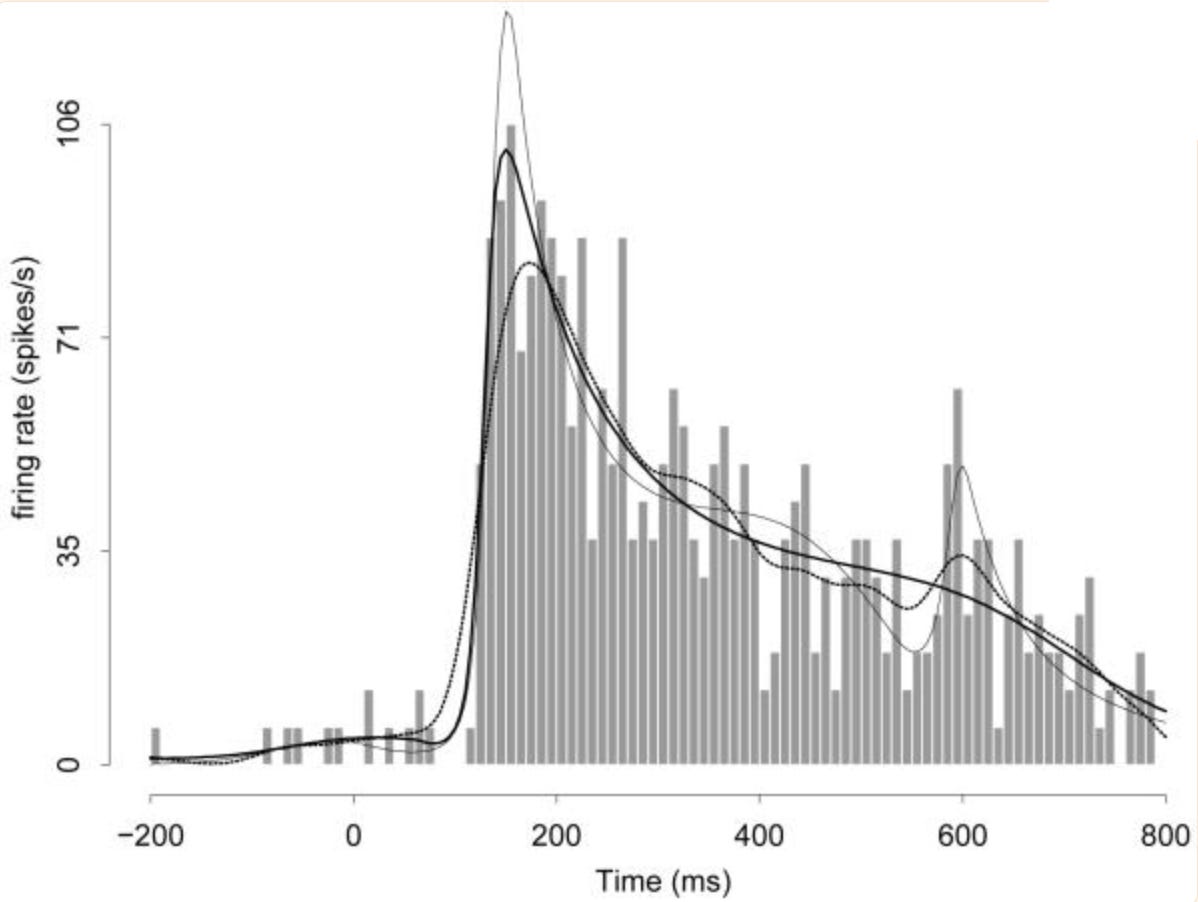
It turns out that neuroscience is filled with problems involving sampling distributions defined on weird objects. A classic example is BARS, a method to fit splines often applied to peri-stimulus time histograms (PSTHs). Here, the goal is to fit a PSTH with cubic splines, for example, to estimate the latency of a neuron. Splines are defined by the set of their knots (discrete objects taking on continuous location values), as well as their weights in a Poisson regression. This gnarly problem was tackled with reversible-jump MCMC, but it could potentially be tackled with gflownets, where the action space would start from just a constant, adding knots until the entire spline is made.
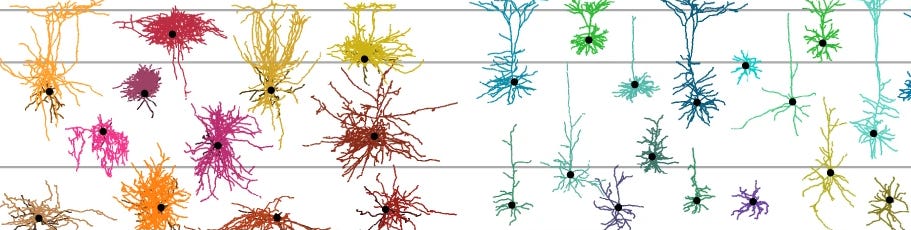
Another more involved example: learning to generate neurons with intricate anatomy. Neurons are naturally represented as discrete graphs embedded in 3D Euclidian space, and can be sampled one branch at a time, starting from the soma. Note that currently, gflownets with action spaces with >100 actions are considered quite hard to sample from, so one would need to limit the complexity of the space in some way.
Similarly, one could use gflownets to fit and sample connectomes. Here, the action space would correspond to adding connections between nodes in a network, e.g. simulated by leaky integrate-and-fire (LIF) units, biophysically-detailed neurons or mean-field neural masses.
You could classify all these applications under the umbrella of neural data science. I think the vision of gflownets is quite a bit larger: they’re motivated, in part, by modelling cognition, with a Bayesian brain/neuro-symbolic/world models flavour. This gets into highly speculative territory, e.g. here’s a paragraph from a tutorial on gflownets from last year:
Brain sciences show that conscious reasoning involves a sequential process of thought formation, where at each step a competition takes place among possible thought contents (and relevant parts of the brain with expertise on that content), and each thought involves very few symbolic elements (a handful). This is the heart of the Global Workspace Theory (GWT), initiated by Baars (1993,1997) and extended (among others) by Dehaene et al (2011, 2017, 2020) as well as through Graziano's Attention Schema Theory (2011, 2013, 2017). In addition, it is plausible (and supported by works on the link between Bayesian reasoning and neuroscience) that each such step is stochastic. This suggests that something like a GFlowNet could learn the internal policy that selects that sequence of thoughts. In addition, the work on GFlowNet as amortized inference learners [4,5,7,9 below], both from a Bayesian [7] and variational inference [9] perspectives, would make this kind of computation very useful to achieve probabilistic inference in the brain. GFlowNets can learn a type of System 1 inference machine (corresponding to the amortized approximate inference Q in variational inference) that is trained to probabilistically select answers to questions of a particular kind so as to be consistent with System 2 modular knowledge (the “world model” P in variational inference). That System 1 inference machinery Q is also crucial to help train the model P (as shown in several of these papers). Unlike typical neural networks, the inference machinery does not need to be trained only from external (real) data, it can take advantage of internally generated (hallucinated) pseudo-data in order to make Q consistent with P.
Boy, that escalated quickly! From my vantage point as a humble non-Turing-award-winner, it seems like another attempt at a Bayesian brain theory with a different amortized inference scheme than the usual variational inference (VI) based one (i.e. FEP). My understanding is that this is still highly conceptual rather than a concrete proposal, but I’m sure this will evolve rapidly.
TL;DR
GFlowNets sample sequentially from unnormalized probability distributions defined on sets and graphs
GFlowNets mix concepts from MCMC and RL
The best sources of information for GFlowNets are workshops and tutorials; read the papers after
They’ve been used for drug discovery and materials science, not yet for neuroscience, but they have a lot of potential.