NeuroAI paper roundup #3: focus on vision
Equivariance in neural networks, retinal computations, emotions, faces, wormholes, topographic neural nets and higher-level processing
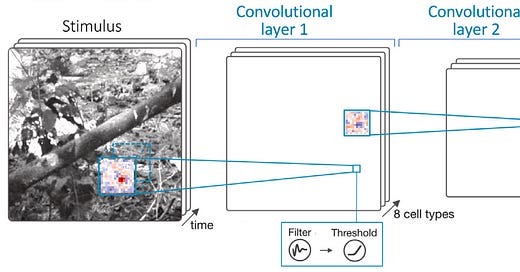
Interpreting the retinal neural code for natural scenes: From computations to neurons
This paper in Neuron showcases some very strong results in modelling the retina and mechanistic interpretability. They fit CNNs to retinal ganglion cells (RGCs) of retinas responding to natural scenes. RGCs are the final stage of processing in the retina; they’re downstream from the rods & cones as well as horizontal and bipolar cells. It turns out that if you just use the outputs of the RGCs to train your network, you get the intermediate units for free: the units in the intermediate layers of the CNNs map nicely to real interneurons in the retina. That means you can use all sorts of mechanistic interpretability tricks to probe the intermediate layers of the model, with confidence that these units map more or less 1:1 to real neurons in the retina.
That’s a very strong form of alignment between artificial and biological neural networks (see this blog post for an overview of the different degrees of alignment between brains and ANNs and what they can be used for). They use this to unravel different circuits in the retina responsible for different nonlinear phenomena fastidiously documented by physiologists over the years. I think if we can bring this level of detail from the sensory periphery to studies of the cortex, we’re in for exciting years ahead.
Robustified ANNs Reveal Wormholes Between Human Category Percepts
In this epically named paper, the authors find adversarial examples for humans. A little bit of background: some of the best neuroAI models of the visual system are adversarially robust, that is, not sensitive to small image perturbations. This seems to align better with human perception than vanilla networks. Still, adversarially robust networks have adversarial examples, just at larger scales (larger epsilon). In this work, they ask a related question, which is whether the adversarial examples of adversarially robust networks also fool humans. And they do! It turns out that the adversarial examples of adversarially robust network perform small image manipulations which can fool humans to switch to a different semantic category (hence, wormholes between categories). Previously, this kind of effect was demonstrated anecdotally using image manipulation (i.e. Photoshop), and it wasn’t clear how far one could push the idea.
I think this is an exciting avenue because it points towards making networks more robust using a careful empirical approach. We can translate the conventional saying “humans are robust to adversarial examples” to a more mathematically precise “humans’ category boundaries are smooth in epsilon balls around examples” to “humans’ category boundaries are mostly smooth in epsilon balls around examples except along dimensions of high curvature corresponding to situation x, y and z”. What are these situations x, y and z? Are humans truly invariant or robust in these situations, or is it an illusion caused by not looking closely enough? The manipulations demonstrated tend to be highly localized, and so perhaps a more refined notion of epsilon-ball will take into account foreground-background distinctions.
End-to-end topographic networks as models of cortical map formation and human visual behaviour: moving beyond convolutions
There is no accepted mechanism by which weight sharing can be implemented in cortex1. That means that the visual cortex cannot literally be a CNN, and therefore must derive its relative spatial stationarity from the statistics of the natural world and genetic and development biases. What the cortex is, instead, is locally connected: neurons lie on a 2d sheet, receive local input, and project to other areas locally. A complete model of cortical visual processing should swap convolutional layers for local layers. It turns out, however, that it’s not that straightforward to implement a locally connected neural network in an efficient way, and most models thus far have only used a single topographic (i.e. locally connected layer), frequently to model V4 → IT.
This paper does it! Swap out the convolutional layers for locally connected layers, train on categorization on ecoset, an ecologically motivated alternative to ImageNet. I was really curious how they managed this feat, because I went down this exact path last year, even going to the extent of dabbling in Triton to compile custom locally connected kernels for PyTorch. The answer, in the methods, sent me into a rage: turns out there’s a function that does this directly in Tensorflow. ¯\_(ツ)_/¯.
They found some really nice topographic maps that look a little like orientation pinwheels in V1. They also found some evidence (pretty weak in absolute terms) for a better match to human visual biases. Now, once we get into models which have non-stationary properties over space and that approximate foveation, I think we have to think a bit more deeply about the visual diet fed into the model. Images in ecoset, on average, have objects centered within images, because people generally point their cameras at things of interest; but it’s not quite the same as saying that what is fed is an approximation of the foveated diet a human gets. I think it’s possible to approximate that diet by cropping images in proportion to the probability of foveating on objects under the crop, using estimates of salience from eye- and mouse-tracking.
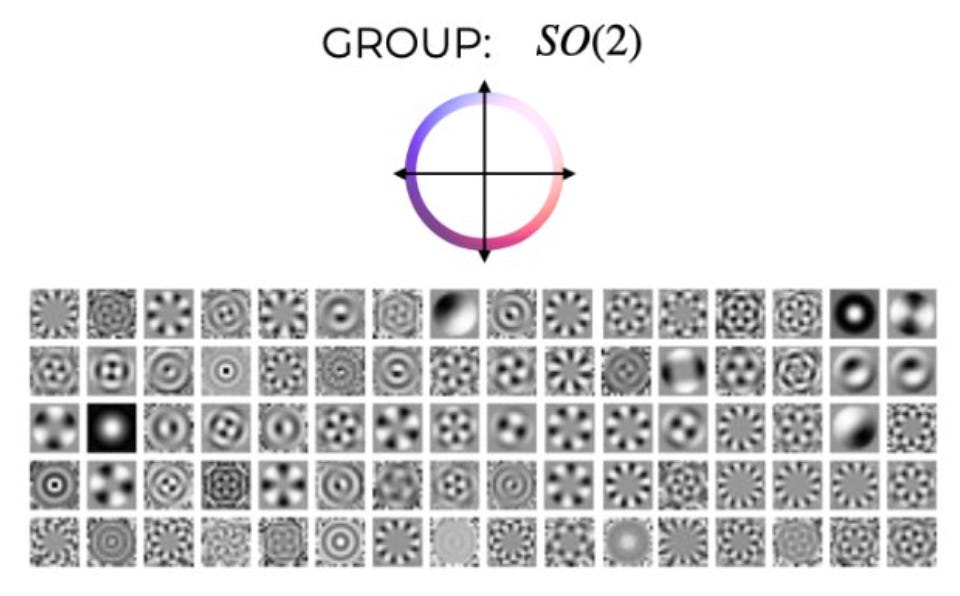
Bispectral neural networks
I heard about this paper from the TWIML podcast, where the first author, Sophia Sanborn did a fantastic job covering a ton of ground in 45 minutes: analytical philosophy, Hubel & Wiesel, sparse coding, group theory, geometric deep learning, and finally, this paper. In Olshausen & Field’s classic work (1996), they found that the responses of neurons in V1 resembled a sparse code for natural images. Hence, there’s a convergence in representation between an optimality principle and the brain.
The work here was motivated by a similar optimality principle, equivariance to identity-preserving transformations. If you translate an image, its power spectrum is preserved; in addition, its phase spectrum maintains a definite set of relationships (i.e. you get a linear phase advance with frequency when you translate). So the Fourier basis is a very good basis for capturing translations. But what about other groups? It turns out that there is a preserved quantity that gets preserved in the Fourier basis under translation, which is the bispectrum. What the authors show is that you can learn the equivalent of Fourier bases on arbitrary groups by imposing that the bispectrum is preserved.
What does that have to do with brains? I think we can connect the dots from Sophia Sanborn’s description of her thesis (which I haven’t been able to find online):
A core hypothesis that I advance in my PhD thesis “A Group Theoretic Framework for Neural Computation” (UC Berkeley, 2021) is that the brain evolved to efficiently encode this transformation structure through the use of group-equivariant representations.
I’m excited to peek more into this field by attending this year’s NeurReps workshop and watching last year’s.
Emergence of emotion selectivity in a deep neural network trained to recognize visual objects
The authors take a look inside a CNN trained on Imagenet and find that there are some units which respond selectively to the valence of a battery of images: neutral, pleasant and unpleasant. They find that ablating these units makes it harder to infer the valence of other items, hence finding a causal role for the units. Thus, perhaps the intrinsic valence of objects can be inferred without needing hardcoding by 1) projecting onto a high-dimensional object space, as might be done by a CNN trained with supervision or self-supervision and 2) downprojecting to some low-dimensional space. The authors conclude that
these results support the idea that the visual system may have the innate ability to represent the affective significance of visual input
That’s an interesting idea. However, I would venture that at least some affective visual biases are baked in; for example, the intrinsic fear of snakes or the attention-grabbing appearance of faces. So while regular visual features from objects may be informative enough to make an affective judgement, where does the mapping from object space to valence come from?
Bonus: The neural code for “face cells” is not face-specific & Medial temporal cortex supports compositional visual inferences
Right as I was about to fire off this newsletter, two papers showed up on my feed. The first is from Marge Livingstone on face cells. It’s a lovely study of the idea that there’s no such thing as pure face cells: these are generic feature detectors that happen to be very good at faces, and they could respond equally well to roundish things with appropriately located holes, e.g. buttons and electrical outlets. They show that you can predict the selectivity of neurons to faces by mapping out their responses to non-faces. Neat!
The second paper from Tyler Bonnen in Dan Yamins’ lab examines the role of the medial temporal cortex in visual perception (MTC), e.g. perirhinal cortex, which feeds into the hippocampus and closely related structures critically important in memory. They cook up visual tasks which are hard for time-limited humans and easy for time-unconstrained humans; they show that DNNs look a lot like time-limited humans; and they show that time-unconstrained humans with MTC damage are a lot like time-limited humans. All in all, this is evidence that there’s something about the MTC that allows higher-level reasoning across saccades to occur. Definitely the start of an interesting research programme.
Although there’s some interesting research on building biologically plausible weight-sharing. See Pogodin et al. (2021).